「凡走過必留下痕跡」，探索動點的軌跡，是電腦圖學科技幫助人們了解數學曲線的利器，總是能讓人有驚艷的發現和感動。就讓我們借助JSXGgraph探索拋物線、橢圓和雙曲線等二次曲線的軌跡。

要觀察動點的軌跡，記得將動點的「trace」屬性設定為true。

拋物線

定義

「與定點F（焦點）的距離等於與定直線L（準線）的距離相等的所有點構成的集合所形成的圖形」

作圖步驟

• 作焦點F。
• 作準線L。
• 作準線L上的動點（P）。
• 作線段PF的中垂線M。
• 作過P點且與L垂直的直線M。
• 作直線M與直線N的交點Q。
• Q點的軌跡便是拋物線。

原理

因為Q在FP的中垂線上，所以三角形QFP為等腰三角形，線段QF等於線段QP，又線段QP垂直於準線L，所以滿足拋物線的定義「與定點F（焦點）的距離等於與定直線L（準線）的距離相等」，所以Q點的軌跡便是拋物線。

值得一提的是，直線M恰好便是點Q的切線。

執行結果如下：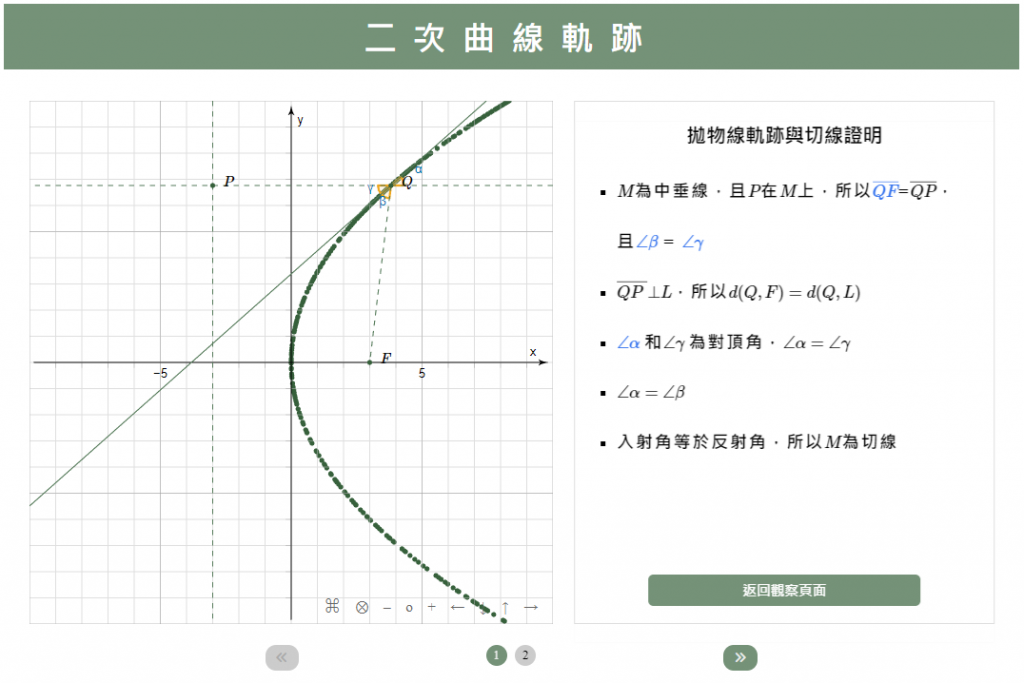

橢圓

定義

「與兩定點F1（焦點1）、F2（焦點2）的距離和為定值所有點構成的集合所形成的圖形」

作圖步驟

• 作焦點F1、F2。
• 以F2為圓心，大於線段F1F2的長度為半徑作圓C。
• 作圓C上的動點（P）。
• 作線段PF1的中垂線M。
• 作直線PF2。
• 作直線M與直線PF2的交點Q。
• Q點的軌跡便是橢圓。

原理

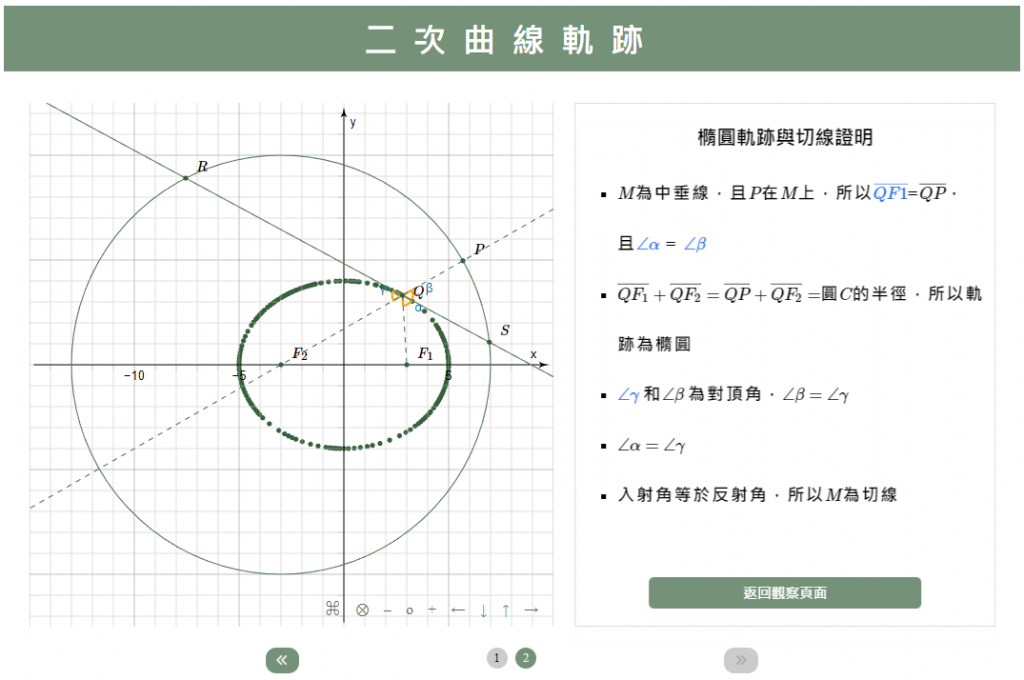
因為Q在PF1的中垂線上，所以三角形QF1P為等腰三角形，線段QF1等於線段QP，又線段QP+線段QF2為大圓半徑，得到線線段QF1+線段QF2恒等於圓C半徑，所以滿足橢圓的定義「與兩定點F1（焦點1）、F2（焦點2）的距離和為定值」，所以Q點的軌跡便是橢圓。

直線M也是點Q的切線。

雙曲線

雙曲線定義是「與定點F（焦點）的距離等於與定直線L（準線）的距離相等的所有點構成的集合所形成的圖形」

雙曲線基本上是橢圓的孿生兄弟，只要將作圖第二步驟的圓C半徑小於線段F1F2即可，想不到圖形如此冗異的兩種圖形，血緣竟如此親近，真是「圖不可貌相」。

程式原始碼

今日程式原始碼

今日小結

其實二次曲線的軌跡製作有很多方法，今天介紹的是最常用的作圖方式，同時也能學習切線的作法。另外，今天設計的網頁中，有加上直線M也是點Q的切線的證明，有興趣的話，可以參考看看，明天見！